作者：林渝修

知識在經濟學的世界裡用途廣泛，舉例來說，效率市場假說中不同強度的效率能將不同程度的私有資訊轉為不同程度的獲利。1974 年諾貝爾經濟學獎得主海耶克（Friedrich Hayek） 1945 年在《美國經濟評論》上發表了一篇名為 The Use of Knowledge in Society 的文章，在其中就強調了價格系統（price system）在傳遞知識上的優勢。價格能將知識「去中心化」的傳遞到社會每個角落，這些資訊能進一步幫助人們用最有效率的方式運用資源。我們這篇文章要討論的則是一種在經濟學中比較特別，但至關重要的知識：共有知識。

共有知識（Common Knowledge）： 你與我都知道某件事，而且你我都知道你我知道某件事，不止如此，你我甚至還知道你我知道你我知道某件事，而「知道」循環會無窮無盡的延伸下去。

藍眼睛難題

除了看了頭很痛外，你可能立即有了個疑問，為什麼要那麼多層的「知道」？你我都知道不就好了嗎？為了在此強調共有知識的無限「知道」循環的威力，我們就在這裡搬出一個經典的邏輯題 - 藍眼睛難題。

有 2 個藍眼睛的人不幸遇難，漂流到一座孤島上，這座孤島上有一個原始聚落，裡面全部人的眼睛都是綠色的。而島上只有一艘船在每天早上會開一班船到文明世界，但這艘船的船長個性非常 GY，他出了一個難題：「告訴我你們自己眼睛的顏色，答對了我再帶你們走。」

但他設定了一個重要的規則： 不准跟任何人談到和眼睛顏色有關的話題。

一聽之下兩個人都愣住了。第一，他們從來沒想過要仔細看自己眼睛的顏色，不能溝通要怎麼獲得自己眼睛顏色的知識？第二，遇難的他們哪來的鏡子看自己的眼睛顏色？

此時船長給了他們兩條線索：

1. 這座島上只有藍眼睛和綠眼睛的人。
2. 島上至少有一個人的眼睛是藍色的。

問題來了，這兩個人有沒有辦法離開呢？有辦法的話，會在第幾天離開呢？（有興趣的讀者請先不要往下滑，自己想想看。）

答案揭曉：聰明的兩人會一起在第二天早上離開。

為什麼呢？其實 Common Knowledge 的維基頁面就有這個例子。這一切取決於相互知識（Mutual Knowledge）和共有知識（Common Knowledge）的重大差別。在船長說出第二句話前，兩個藍眼睛的人都知道島上至少有一個人的眼睛是藍色的，但他們並不知道對方知道，經濟學上稱呼這種知識為相互知識。另一方面，在船長說出關鍵的線索後，這個知識就成為了共有知識，這也成為了他們能離開的重要關鍵。

協議定理(Aumann’s Agreement Theorem)

共有知識的定義中對於「知道」某件事的條件下了很強的限制，而在這種限制之下我們可以得到許多有趣的定理。我們先將定理本身暫且擱置，來弄清楚協議定理的「協議」是什麼？（以下有電影雷）

在《2009 月球漫遊》這部電影之中，主角以複製人的身份甦醒，保有一套「完全相同」的記憶和生活體驗。假設今天有兩個複製人一起醒來，並各自過了不同的一天，突然對某項工作該怎麼做產生了不同的意見。理性的他們開始互相傾吐，把兩個人一天中所接觸到的資訊都轉為兩人的共有知識。問題來了，在這樣的資訊更新完後，他們還有可能看法不一致嗎？

協議定理告訴你，在經濟學的世界裡，他們的看法在交流完後必定是一致的！

2005 年的諾貝爾經濟學獎得主，以色列經濟學家 Robert Aumann 是第一個用嚴謹數學語言定義共有知識的人，Aumann 同時也在他 1976 年的論文 “Agreeing to Disagree” 中提出了協議定理。 一言以敝之，兩個握有完全相同資訊的理性人在各自有不同經歷後，只要將彼此的經歷轉為共有知識，就必定會達成協議，不會有意見不一致的情況發生。

你們同意彼此的不同意？

協議定理：

假設兩個理性的人在某個情況 \(\omega\) 下，各自在某個知識結構下認為某個事件 \(E\) 發生的事後機率分別為 \(q_i\) 和 \(q_j\)，且這件事和知識結構為兩人的共有知識，那麼 \(q_i = q_j\)。

看了敘述有看沒有懂嗎？讓我們避開共有知識的數學定義和繁雜的集合論語言，試試看用高中數學將協議定理的直覺解釋給你聽。

傳統經濟學界在處理人的知識結構時都以集合概念來描述世界的狀態，而這其實與高中機率的樣本空間概念十分相近。 讓我們設想 2020 大選的情境，假設理性的 A 和 B 都對選舉很有興趣，而且同樣的認為選舉只有七種可能的情境。世界真實的情境只會是其中之一，但 A 和 B 現在還不太確定是哪個，不過他們都同意七種情境個別發生的機率是多少。與機率語言相互對應，世界的狀態空間即為樣本空間 \[ \Omega = \{ \omega_i,\ i = 1,…,7 \} \] 而任何一個世界真實情境都是樣本空間中的一個元素。（如下圖 1）

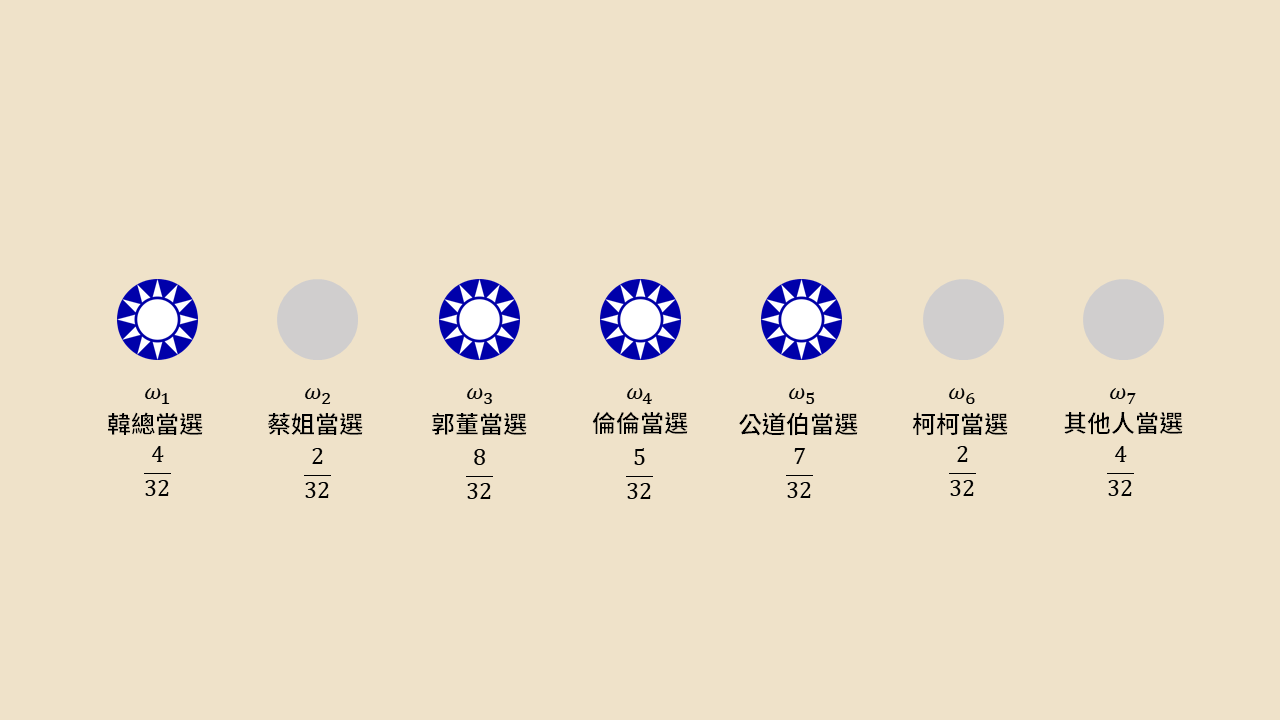
讓我們再進一步假設他們都只在乎 KMT 當選的機率，因此只想知道事件 \( E = \{ \omega_1, \omega_3, \omega_4, \omega_5 \} \) 所發生的機率。在現有的設定下可以很自然地斷定事件 \( E \) 發生的機率是 \(75 %\) 。

\[ P(E) = P(\omega_1) + P(\omega_3) + P(\omega_4) + P(\omega_5) = \frac{24}{32} = 75 % \]

但 A 和 B 還是不太滿意這個結果，於是決定要各自上網了解一下現在的選情，在這樣做後，讓我們假設他們擁有了各自不同的知識結構。（如下圖 2）

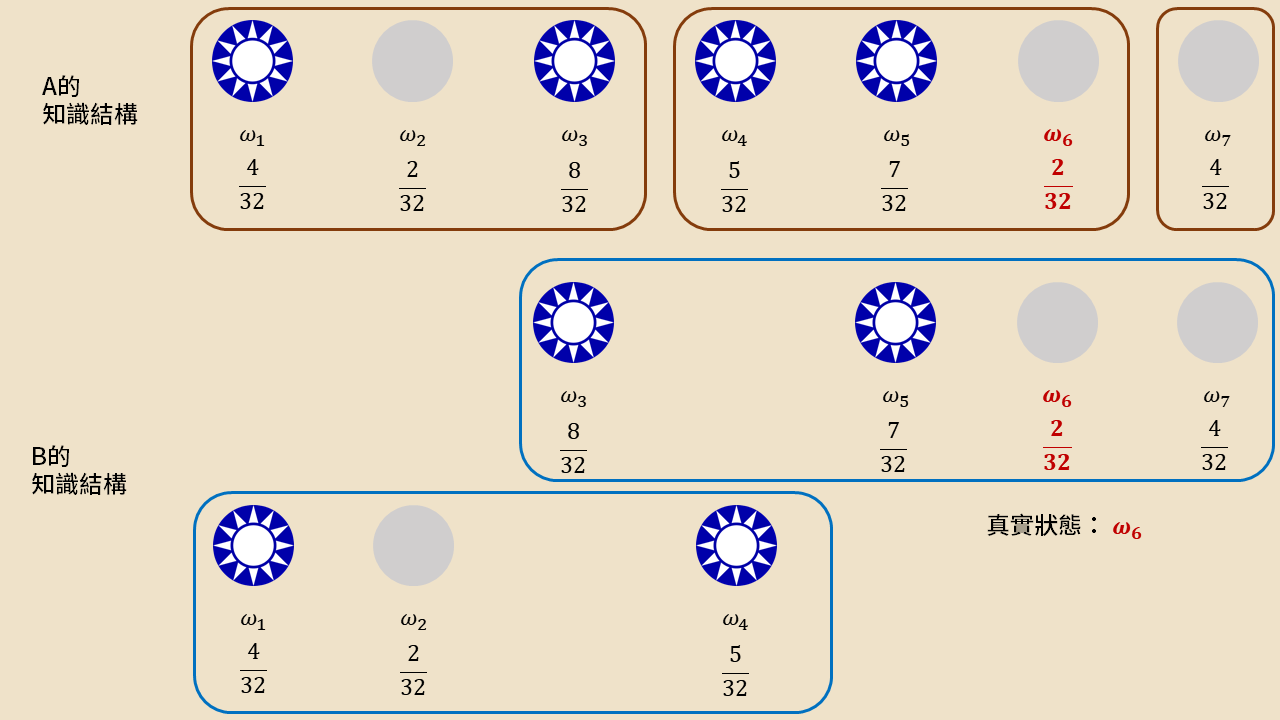
這個知識結構該如何詮釋呢？首先讓我們解釋一下上述的事件是什麼意思。事件可以理解成，這個事件在任何一個元素是真實情境時都成立。舉例來說，在 KMT 當選的事件 \(E\) 中，無論真實情境是 \(\omega_1, \omega_3, \omega_4, \omega_5 \) 其中的哪一個都會成立，因此事件 \(E\) 就是這四個元素所成的集合。

知識結構以數學語言來描述，則是對這個世界的七種狀態使出集合劃分（Partition）。也就是說，有鑒於人們有時候資訊並不充足到能分辨每個情境，卻沒有無知到什麼都無法分辨，我們因此用集合劃分來描繪人對於自己身處在哪個事件中的認知能力。讓我們回到 A 的知識結構來解釋它的意思，讓我們假設世界真實的情境是 \(\omega_6\)，這樣看來 \(\omega_6\) 包含在 A 知識結構中的 \(I = \{ \omega_4,\omega_5, \omega_6 \} \) 事件中，因此雖然 A 不知道真實情境是柯柯當選，A 也能推理出，當選的一定是倫倫、公道伯或柯柯其中之一。

有了對知識結構的認知後，我們沿用世界真實情境為 \(\omega_6\) 的假設，讓我們用條件機率算算看 A 現在認為事件 \(E\) 發生的機率應該會是多少。

\[ P(E|I) = \frac{P(E \cap I) }{P(I)} = \frac{ P({\omega_4, \omega_5 }) }{ P( {\omega_4,\omega_5, \omega_6}) } = \frac{12}{14} \]

接下來讀者可以算算看 B 認為 \(E\) 發生的機率，應該是 \(\frac{15}{21}\)。這兩個值就成為了定理中的 \(q_i\) 和 \(q_j\)，這時你會問，奇怪？這兩個不相等啊！定理想必是搞錯了吧？

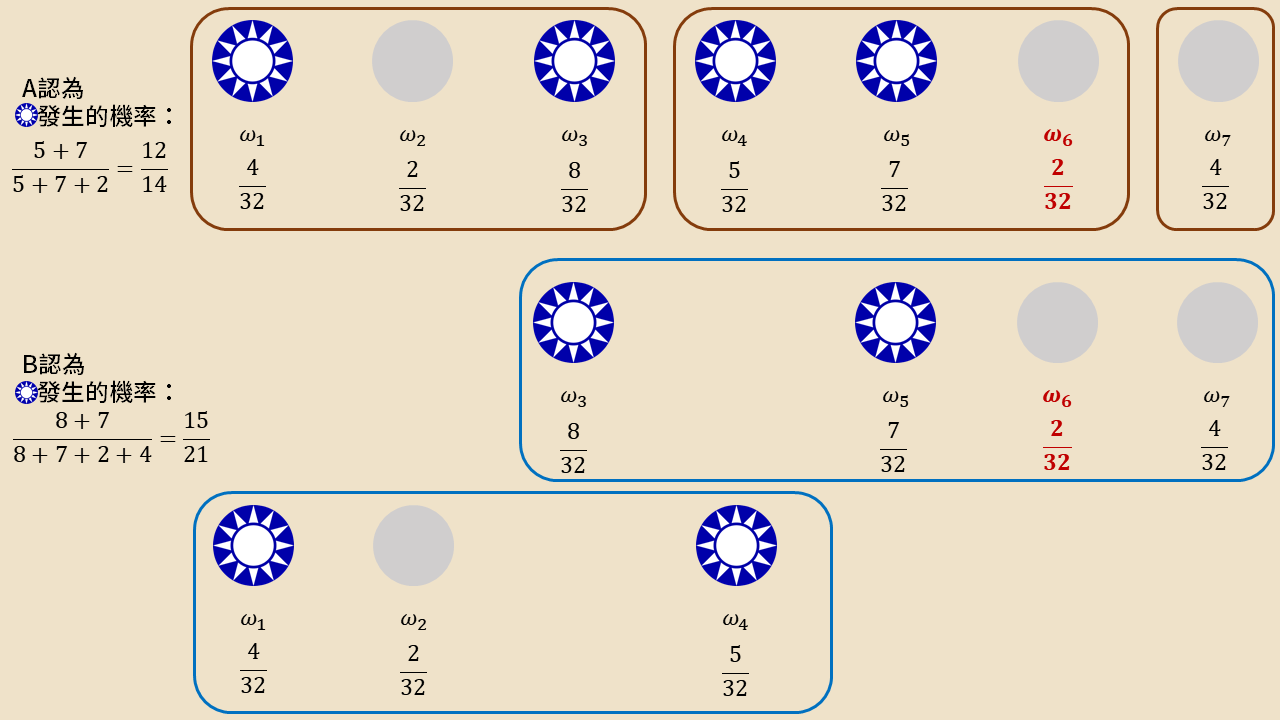
但年輕人終究是年輕人，這裡要注意，知識結構和機率都是共有知識。從 B 的視角來看，他會想如果今天真實情境是 \(\omega_7\)，那麼 A 應該會回報 \(P(E) = 0\) 吧？既然不是，那麼 B 就猜想真實情境必定不是其他人當選，但注意到了，\(\omega_7\) 在 B 計算條件機率時的分母集合之中呢！於是在將 \(\omega_7\) 從原先的集合中分離出來後，B 有了一個新的更新機率 \(\frac{15}{17}\)。用類似的概念， A 也會推得如果是倫倫當選，那機率回報的機率不應該是\(\frac{15}{17}\)，於是 A 也將自己的機率更新為 \(\frac{7}{9}\)。

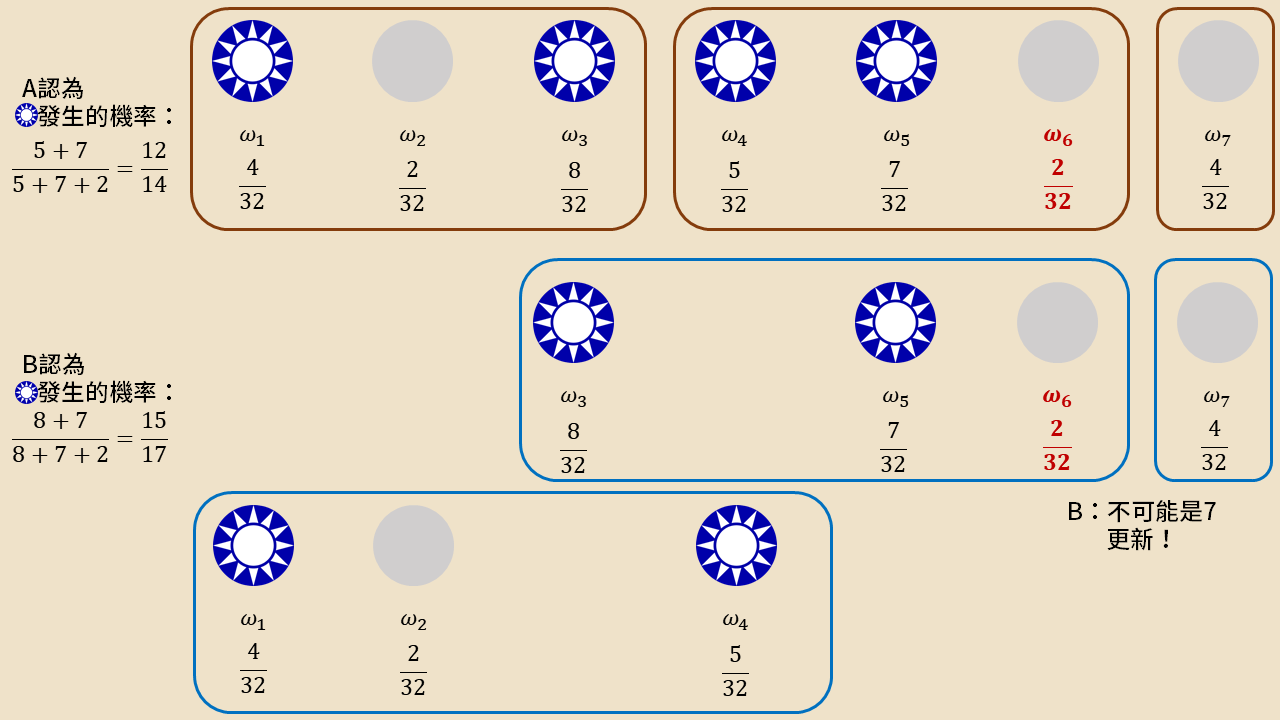
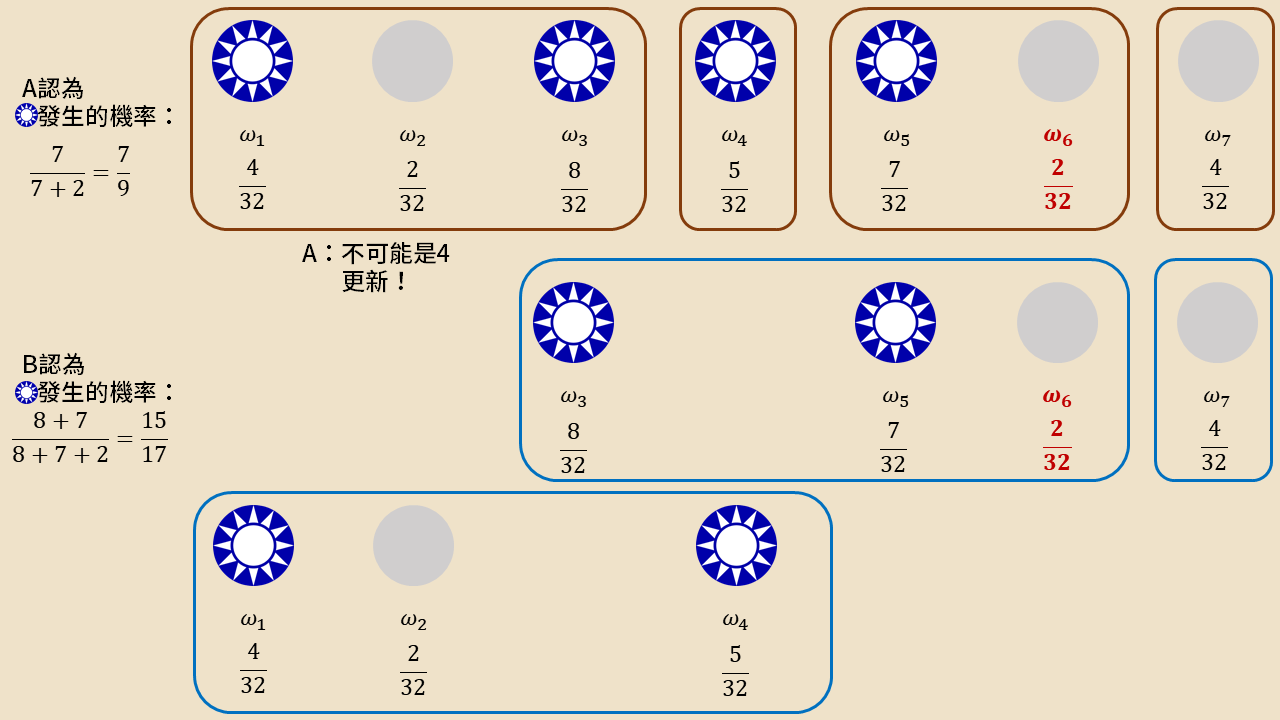
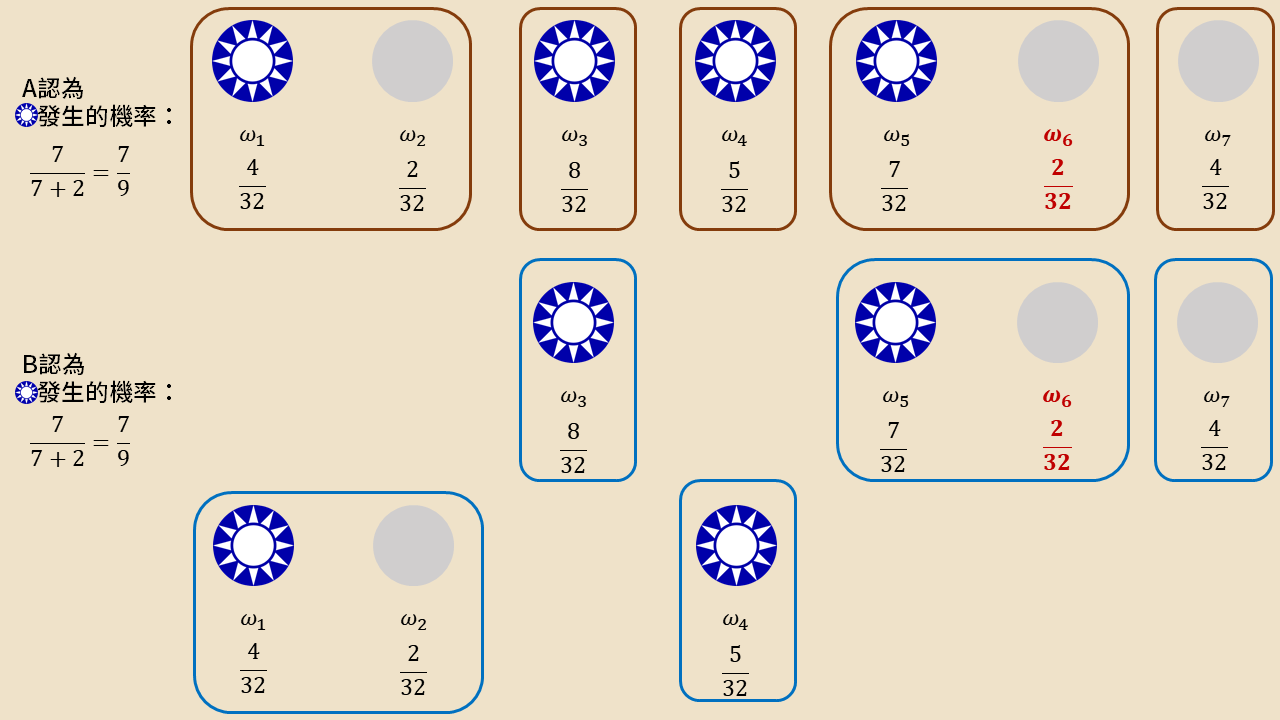
此時兩人的機率還是不同，所以定理果然還是錯了吧？還沒，讓我們複習一下，B 的共有知識究竟有幾層？無限層！因此，B 知道 A 知道 B 的知識結構和更新後機率，因此 B 可以再藉由 A 藉著 B 更新後的知識結構再做一層推理，斷定郭董當選是不可能發生的，於是在將彼此的資訊交換完後，B 會得到最終的 E 發生機率 \(\frac{7}{9}\)。（此例子借用自 Agreeing to Disagree: Survey，讀者可以動動腦將省略的過程想清楚，想累了再查閱該文章對答案）

不可能一致？So what?

乍看之下你或許會問，這樣又怎樣呢？數學上很正確，而且更新資訊使得看法達成一致蠻合理的啊！更重要的是，這實在是個振奮人心的消息，畢竟對於事件的看法不同常常引發很多的紛爭。經濟學（或該說數學？）告訴你，只要兩人都是理性的，且兩人願意將彼此的看法開誠布公地轉為共有知識，兩人對於一個事件的看法必定會是一樣的。因此下次在餐廳（或是家裡客廳）聽到跟你某些立場相左的言論後，只要相信著你和他都是理性的，你就可以走上前去好好的與那個人交流看法，也許你們會因此更新彼此的看法，從而得出兩人都滿意的結果來。

但這其實也是一個蠻違反經濟直覺的結果。畢竟經濟學的重要假設之一就是人都是理性的，但我們同時也會在市場上看到許多看法相左的投資人進行交易來對賭彼此的資訊。另外一個例子，許多金融機構中的分析師，明明使用公司的電腦獲得一樣的資訊，每天晨會也都把彼此所知轉換為共有知識，卻還是會寫出天差地遠的股價報告。因此我們的觀察告訴我們，理性的人應該會在某種程度上有辦法達成意見不一致才對。

進一步地說，許多現代經濟學的研究都是以賽局為模型，但正如同白經濟 〈NBA 轉隊疑雲：共有知識與 Email 遊戲〉 裡所介紹的，共有知識是納許均衡成立的重要假設之一。同時，如道德危機（Moral Hazard）和逆選擇（Adverse Selection）等問題都建立於資訊不對稱（Information Asymmetry）上。如果在賽局的架構下討論這些問題，理性的人在共有知識下看法又必定一致，那麼資訊究竟要在哪裡不對稱呢？

這個定理啟發了許多對於經濟學、哲學和電腦科學的研究，其中一個就是財務經濟學中最著名的定理之一 —— 無交易定理（No-Trade Theorem）。這個定理由經濟學家 Paul Milgrom 和 Nancy Stokey 在他們 1982 年的論文 Information, Trade and Common Knowledge 所提出，並且從此之後就為現代財務經濟學立下了一個嚴峻的挑戰。

To Trade or Not to Trade？

在協議定理中，我們強調了理性的人會互相推估對方的資訊從而更新自己的資訊，最終達到平衡，無交易定理也提出雷同的概念。以經濟學的語言來說，無交易定理告訴我們，如果初始的市場狀態已經達成效率最佳的帕雷圖最適，且市場上的人對於市場中的知識是一致的，更重要的是如果「交易」這個動作是共有知識，那麼即使今天你突然持有某個私有資訊，這個資訊可以讓你在現在的市場價格下獲得交易利潤，交易也不會發生。

現在讓我們用與協議定理相似的邏輯來了解無交易定理背後的直覺。想像一下一位理性投資人身處在一個完美的市場中，所有人對於自己持有的部位都非常滿意，也因為日夜的辛勤研究而對市場本身有「一樣充足」的了解。某天在路上媽祖突然顯靈對這位投資人說：「買 A 股票會發大財！」深信不疑的他立刻拿起手機準備要下 A 股票的單。但這時她突然有了一個疑問：「如果我買，那誰要賣？大家應該都對自己持有的部位很滿意才對啊！」

聰明的投資人想了一下發現一個嚴重的問題，如果有人願意賣給他，代表賣的人看到了 A 股票的利空。既然交易作為共有知識，任何一個人都會在看到交易時合理推測出有人正握有特別的資訊。因此除了別人推測出賣的人有利空消息外，賣的人也會推測想買 A 股票的人知道 A 股票會發大財。這樣來來去去的推理後，聰明的投資人會發現，即使媽祖托夢給他，買賣 A 股票要嘛沒賺頭，要嘛根本沒人要接手，於是就把手機收起來了。

無交易定理問世後丟出了一些有趣的問題，像是：在理性預期的假設下，既然不會有交易，那資訊該如何反應在價格上？（效率市場假說 QQ）另一方面，既然持有資訊沒辦法獲利，那到處做研究報告的金融從業人員又在幹嘛呢？（商管學院 QQ）

這些問題在財務金融的研究上影響甚鉅，許多財務經濟學家都在找不同的模型，讓交易能夠在理性預期的假設下發生。有接觸過金融產品訂價相關理論的人可能有在財務金融論文中看到一個重要假設：市場上必須要有一個被稱為流動性交易人（Liquidity Trader）的角色，他扮演的角色就是基於某種外生給定的衝擊，可能是單純的很渴想買杯水喝但窮得只剩下股票，而必須在市場上不考慮金額買或賣股票。這個角色的存在的一個重要目的就是為了解決無交易定理所提出 —— 沒人願意買或賣 —— 的難題。

結語

知識相關的研究在各個領域中不勝枚舉，而我們今天著重的則是其中比較基礎的問題。作為基礎理論，它們當然與現實有部分脫節，但它仍然是經濟學討論中必須存在的框架。介紹這樣的理論除了讓對經濟學有興趣的人接觸其中比較技術性的語言外，也希望能讓讀者在未來面對各種決策問題時能停下來多想一會。舉例來說，有沒有可能有某個人在你準備進行交易時，正握有特別的資訊，正準備從衝動的你手上海撈一筆呢？

參考資料

1. Friedrich August von Hayek, “The Use of Knowledge in Society,” American Economic Review, XXXV, No. 4; September, 1945, pp. 519–30
2. Wikipedia, Common Knowledge(logic)
3. R. Aumann, Agreeing to Disagree, Ann. Statist. 4 (1976), pp.1236~1239
4. G. Bonanno and K. Nehring, Agreeing to Disagree: A Survey, UC Davis (1997)
5. P. Milgrom and N. Stokey, Information, Trade and Common Knowledge, Journal of Economic Theory 26. (1982) pp.17~27